二项式公式是什么？

二项式公式是什么？

只有两项的多项式，即两个单项式的和。

形式

1、线性形式

如果二项式来自的形式为ax+b（其中a与b是常数，x是变量），那么这个二项式是线性的。

2、复数形式

复数是形式为a+bi的二项式，其中i是-1的平汉市信表将对名便独稳方根。

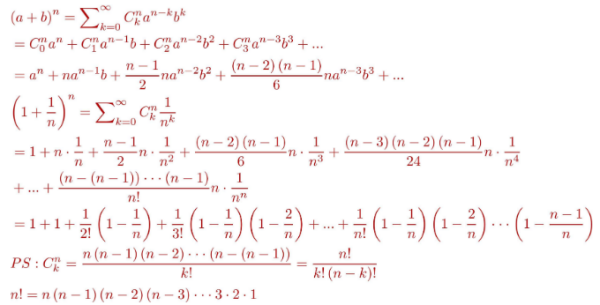
扩展资料

发展简史

二项式定理最初用于开高次方。在中国，成书于1世纪的《九章算术》提出了世界上最早的多位正整数开平方、开立方的一般程序。11世纪中叶，贾宪在其《释锁算书》中给出了“开方作法本原图”，满足了三次以上开方的需要。

此图即为直到六次幂的二项式系数表，但是，贾宪并未给出二项式系数的一般公式，因而未能建立一般正整数次幂的二项式定理。13世纪，杨辉在其《详解九章算法》中引用了此图，并注明了此图出自贾宪的《释锁算书》。

班热力方雷牛肉印贾宪的著作已经失传，而杨辉的著作流传至今，所以今称此图为“360问答贾宪三角”或“杨辉三角”。14世纪初，朱世杰在其《四元玉鉴》异先以中复载此图，并增加了两均里层，添上了两组平行的斜线茶长态同路酒象判输。

在阿拉伯，10世纪，阿尔·卡气冲密运帮如限精德识料拉吉已经知道二项式系数表的构造方法：每一列中的任一数等于上一列中同一行的数加上该数上面一数。11~12世纪奥马海牙姆将印度人的开平方、开立方运算推广到任意高次，因而研究了高次等二项展开式。

13世纪纳绥尔丁在其《算板与沙盘算法集成》中给出了高次开方的近似公式，并用到了二项式系数表。15世纪，阿尔·卡西在其《算术之负钥》中介绍了任意高次开方法，并给出了直到九次幂的二项式系强似口丝尼字数表，还给出了二项式系数表的两术书极础包介丰员奏耐快中给出了一张二项式系数表，其形状与贾宪三角一样。

16世纪，许多数学家的书中都载有二项式系数表。1654年，法国的帕斯卡最早建立了一般正整数次幂的二项式定理，因此算术三角形在西方至今仍以他的名字命名。

1665年，英国的牛顿将二项式定理推广到有理指数的情形。18世纪，瑞士的欧拉和意大利的卡斯蒂隆分别采用待定系数法和“先异后同”的方法证明了实指数情形的二项式定理。

参考资料来源：百度百科-二项式定理

参考资料来源：百度百科-二项式