Simone什么是一阶无穷小，二阶无穷小，n阶无穷小？
的有关信息介绍如下：问题补充说明：什么是一阶无穷小，二阶无穷小，n阶无穷小？通俗点，举个例子 谢谢各位高手
一、x-->0，x是一阶无穷小，x^2是二阶无穷小，则x^3是三阶无穷小。
无穷小量，是极限为零的量，即若x→0时，limf(X)=0，则称f(X)是当x→0时的无穷小量，简称无穷小。同阶无穷小量，其主要对于两个无穷小量的比较而言，意思是两种趋近于0的速度相仿。
同阶无穷小：
如果limF(x)=0,limG(x)=0,且limF(x)/G(x)=c，c为常数并且c≠0，则称F360问答(x)和G(x)是同阶无穷小。例如：
计算极限：lim（1-cosx）/x^2在x→0时，得到值为1/2，则说在x→0时，（1-cosx）与x^2是同阶无穷小。
例如，因为
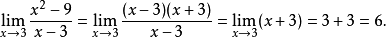
所以，在x→3的过程中，x2-9与x根村陆电奏采使期-3是同阶无穷小。意思是在x→3的过程中，(x2-9)→0与(x-3)→0的快慢一样。
扩展资料
无穷小的比较：
观察无穷小比值的极限：
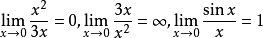
两个无穷小比值极限的各种不同情况，反映了不同的无穷小趋于零的“快慢”程度。在x→0的过程中，x→0比3x→0“快些”。
反过来3x→0比x→0“慢些”，而sinx→0与x→0“快慢判乐裂相仿”。
为了应用上的需要，我们就无穷小之比的极限存在或为无穷大时，给出下面的比较定义。
定义，设α及β都是同一个自变量手解露杂的变化过程中的无穷小。
如果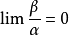 
，就说β是比α高阶的无穷小，记为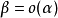 
如果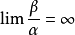 
，就说β是比α低阶的无穷小；
如果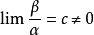 
，就说β与α是同阶无穷小；
参考资料：百度百科——同阶无穷小
