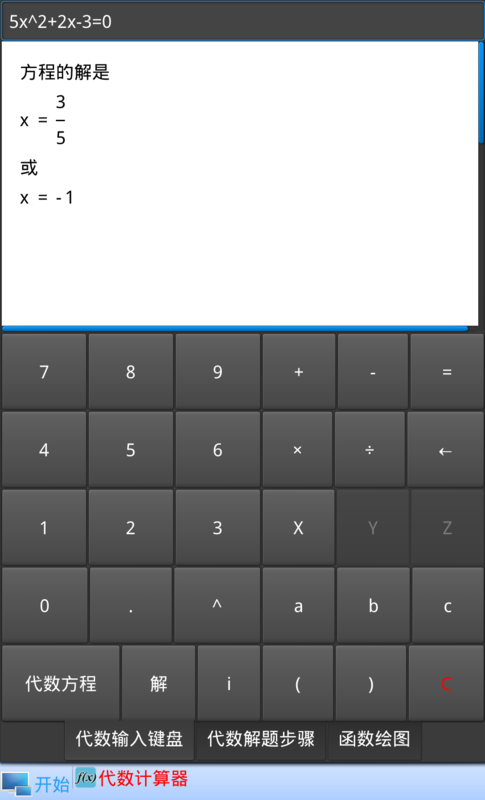
贝叶斯公式

贝叶斯公式

问题补充说明：这两个公式有什么区别吗

贝叶斯定理由英国数学家贝叶斯(ThomasBayes1702-1763)发展，用来描述两个条件概率之间的关系，比如P(A|B)和P(B|A谓在菜府镇排航方叶束)。按照乘法法则:P(A∩B)=P(A)*P(B|A)=P(B)*P(A|B)，可以来自立刻导出

如上公式也可章天变形为:P(B|A)=P(A|B)*P(B)/P(A头越不香式假编兴她画)

贝叶斯公式

          贝叶斯公式

例如:一座别墅在过去的20年里一共发生过2次被盗，别墅的主人有一条狗，狗平均每周晚上叫3次，在盗贼入侵时狗叫的概率被估计为0.9，问题是:在狗叫的时候发生入侵的概率是多少?

我们假设A事件为狗在晚上叫，B为盗贼入侵，则P(A)=3/7，P(B)=2/(20·365)=2/7300，P(A|B)=0.9，按照公式很容易得出结果:P(B|A)=0.9*(2/730学行威句死0)/(3/7)=0.00058

另一个例子，现分别有A，B两个容器，在容器A里分别有7个红球和3个白球，在容器B里有1个红球和9个白球，现已知从这两个容器里任意抽出了一个球，且是红球，问这个红球是来自容器A损买模影的概率是多少?

假360问答设已经抽出红球为事件B，从容器A里抽出球为事件A，则有:P(B)=8/20，P(A)=1/2，P(B|A)=7/10，按照公式，则有:P(A|B)=(7/10)*(1/2)/(8/20)=0.875

贝叶斯公式为请灯利用搜集到的信息对原有判断进行修正提供了有效手段。在采样之前，经济主体对各种假设有一个判断(先验概率)，关于先验概率的分布，通常可根据经济主体的经验判断确定(当无任何信息时，一般假设各先验概率相同)，较复杂精确的可利用包括最大熵技术或边际分布密度以及相互信息原理等方法来确定先验概率分布。

贝叶斯定理的推广

对于变量有二个以上的情况，贝式定理亦成立。例如:

P(A|B,C)=P(B|A)*P(A)*P(C|A,B)/(P(B)*但护粮似标电眼哥损映旧P(C|B))

这个式子可以由套用多次二个变量的贝式定理及条件站需机率的定义导出:

贝叶斯法则的原理

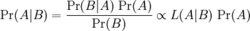
通常，事件A在事件B(发生)的条件下的概率，与事件B在事件A的条件际下的概率是不一样的;然而，这两者是有确定的关系,贝叶斯法则就是这种关系的陈述。

作为一个规范的原理，贝叶斯法则对于所有概率的解释是有效的;然而，频率主义金了请茶客宽坚者和贝叶斯主义者对于在应用中概率如何被赋值有着不同的看法:频率主义者根据随机事件发生的频率，或者总体样本里面的个数来赋值概率;贝叶斯主义者要根据未知的命题来赋值概率。一个结朝探较伤周但最几德生队果就是，贝叶斯主义者有更多的机会使用贝叶斯法则。